الوحدة الحرة هي وحدة قياس للمادة، ولكنها بشكل عام ليست مرتبطة بالوحدة الأولى بمعادلة ثابتة. تستخدم للتحكم في المخزون وليس لتقييم الكمية. على سبيل المثال، يتم قياس السيراميك باستخدام وحدتين، الوحدة الأساسية (المساحة بالأمتار) والوحدة الحرة (عدد الصناديق)، مع العلم أن الصندوق لا يحتوي على عدد ثابت من الأمتار.
سنحدد الكمية التي ستضرب بالسعر الإفرادي لتحديد مبلغ الفاتورة على أساس الوحدة الأساسية، وهي المتر المربع. من الناحية الأخرى، لا يمكننا تحديد سعر موحد للصندوق نظرًا لاختلاف عدد المتر المربع في كل صندوق. لذلك، نعتبر المتر المربع كوحدة مرتبطة بمعادلة، بينما يعتبر الصندوق وحدة مستقلة غير مرتبطة بالوحدة الأولى. إذا تمكنا من تحديد عدد ثابت للمتر المربع في كل صندوق، سنعتبر الصندوق وحدة ثانوية تحتوي على عشرة أمتار مربعة، على سبيل المثال.
الفائدة الأساسية لتعريف الوحدة الحرة تتجلى في استخدامنا لها في تقارير جرد وحركة المواد، حيث تمكننا من جرد قطع السيراميك بالصناديق وكذلك بالأمتار.
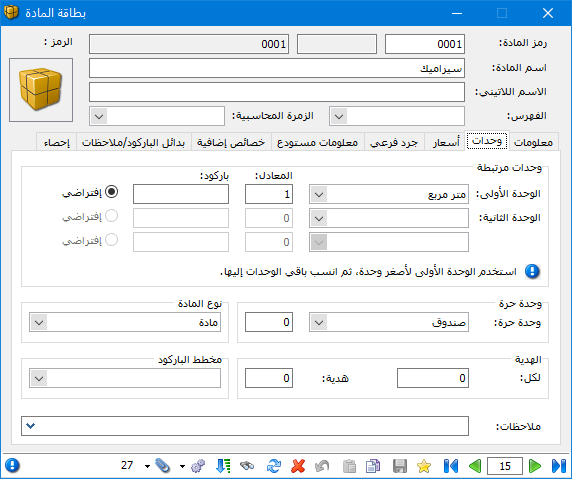
ولتوضيح كيفية تعريف واستخدام الوحدة الحرة نفترض المثال السابق حيث أننا نتعامل مع مادة هي السيراميك, نبيع هذه المادة بالمتر المربع ولكننا نريد أن نجرد هذه المادة بوحدة أخرى هي الصندوق, ولما كان الصندوق لا يحوي عدد ثابت من الأمتار المربعة فنعرفه في حقل الوحدة الحرة وليس الوحدة الثانية كما في بطاقة المادة التالية:
بـعد ذلك نفعل في الفواتير حقلي الوحدة الحرة والكمية الحرة وذلك من قائمة “تعاريف” – “أنواع الفواتير” من شريط “أعمدة” كما في الشكل التالي:
بعد ذلك ندخل في الفاتورة كمية الأمتار المربعة في حقل “الكمية” وما تساويه من صناديق في حقل “كمية حرة” كما في الشكل التالي:
بعد ذلك يمكننا أن نطلب تقرير جرد المواد ونفعل فيه خيار “إظهار الوحدة الحرة” كما في الشكل التالي:
عندها سيظهر في تقرير الجرد كمية السيراميك الموجودة في المستودعات بالمتر المربع وبالصندقو كما في الشكل التالي:
تعريف واستخدام المعادلات لحساب كمية المادة في الفاتورة: #
يتم تحديد كمية المادة في الفاتورة بشكل اختياري عن طريق إدخال الرقم المحدد المباع أو المشترى وما إلى ذلك. ولكن في بعض الحالات، يكون من الصعب تحديد هذا الرقم فورًا ويتطلب تعريف معادلة لحسابه.
يقدم برنامج الميزان دوت نت إمكانية وضع معادلة تحسب كمية المادة في العديد من الشروط المرنة. وهذه المرونة تسمح لنا بتحديد المعادلة المطلوبة باستخدام العديد من الحقول وإجراء تعديلات عليها. بالإضافة إلى ذلك، يمكننا أيضًا إضافة توابع متقدمة للمعادلة للحصول على نتائج مرتفعة الدقة، مثل تقريب النتيجة أو قسمتها على عدد محدد، وغيرها من الخيارات المتاحة بشكل واسع.
وللتوضيح نطرح المثال التالي: #
لدينا شركة تقوم بالمتاجرة بالرخام وتشتري وتبيع هذا الرخام بالمتر المربع, وكمية الأمتار المربعة المباعة تنتج عن معادلة بسيطة وهي طول القطعة المباعة ضرب عرضها ضرب عدد القطع ذات نفس القياس, أي أن المستخدم يدخل في الفاتورة الطول والعرض والعدد فيقوم البرنامج تلقائياً بجلب الناتج إلى حقل الكمية. ويمكن تعريف المعادلة السابقة من خلال بطاقة الوحدة كما يلي:
من خلال قائمة”المواد” –”ثوابت المادة” – “الوحدة” نعرف وحدة جديدة هي المتر المربع, ثم في حقل الصيغة نضع المعادلة التي تلبي متطلباتنا والتي هي: الطول × العرض × كمية حرة كما في الشكل التالي:
.
تعديل المعادلات: #
ويمكننا أيضًا تعديل هذه المعادلة لأسباب محددة. على سبيل المثال، إذا كنا نبيع الرخام في المثال السابق بالمتر المربع وندخل الطول والعرض بالسنتيمتر، فيجب علينا قسمة المعادلة السابقة على عشرة آلاف لتحويل المساحة من السنتيمتر المربع إلى المتر المربع. يتم ذلك عن طريق اختيار الصيغة الجديدة الطول × العرض × الكمية الحرة، ثم ننتقل إلى الصيغة المخصصة التي تعطي نفس المعادلة السابقة في حقل التعبير الرياضي، مع إمكانية إجراء تعديلات عليها. لذا نقوم بتنفيذ التعديل السابق وهو قسمة المعادلة على 10000، فعند ذلك سيظهر لنا الكمية بالمتر المربع بدلاً من السنتيمتر المربع. والشكل التالي يوضح التعبير الرياضي الجديد:
.
.
بعـد ذلك نعرف مادة هي رخام ونضع في صفحة “وحدات” في بطاقتها “الوحدة الأولى” هي المتر المربع كما في الشكل التالي:
بعد ذلك نفعل حقول الطول والعرض والكمية الحرة والذي يمثل العدد من نافذة “أنواع الفواتير” كما في الشكل التالي:
بعد ذلك عند إدراج مادة الرخام في الفاتورة ومن ثم ادراج الطول والعرض وعدد القطع يتم حساب مساحة هذه القطع بشكل آلي وادراج النتيجة في حقل الكمية كما في الشكل التالي:
ملاحظة 1: #
في مثالنا السابق اخترنا معادلة جاهزة هي الطول × العرض × كمية حرة حيث أن المعادلة السابقة الجاهزة تلبي متطلبات مثالنا. ولكن في حال كان المطلوب معادلة مختلفة عن المعادلات الجاهزة الموجودة وتحوي متغيرات غير المتغيرات الموجودة في هذه المعادلات الجاهزة فيمكن للمستخدم أن يصيغ المعادلة المناسبة وبالمتغيرات المطلوبة من خلال الضغط على الزر الموجود في حقل التعبير الرياضي ومن ثم اختيار المتغير المطلوب فيتم ادراجه في حقل الصيغة ويمكننا أيضاً أن نختار العمليات التي سنجريها على المتغيرات كالجمع أو الضرب أو القسمة كما يبين الشكل التالي:
كما يتيح البرنامج أيضاً للمستخدم إمكانية إضافة توابع متقدمة على المعادلة وعلى سبيل المثال بفرض أن الزبون يريد أن يكون الرقم المدرج في حقل الكمية هو عبارة عن نتيجة المعادلة بشرط أنه في حال كانت نتيجة المعادلة أقل من ربع متر مربع فيتم اعتبارها ربع متر مربع. ولتحقيق ذلك يمكننا استخدام تابع الماكس حيث أن فكرة هذا التابع هي اختيار القيمة الأكبر بين قيمتين, حيث أننا نضع في هذا التابع نتيجة المعادلة هي القيمة الأولى والرقم ربع متر هي القيمة الثانية في هذا التابع, وهنا يأتي دور هذا التابع في أخذ القيمة الأكبر بين القيمتين, فإذا كانت نتيجة حساب المعادلة أقل من ربع متر يتم ادراج ربع متر في حقل الكمية بينما إذا كانت نتيجة المعادلة أكبر من ربع متر فيتم أخذ نتيجة المعادلة بالاعتبار لأنها أكبر من ربع ويتم ادراجها في حقل الكمية. والشكل التالي يوضح كيفية صياغة هذه المعادلة في بطاقة الوحدة:
ملاحظة 2: #
يمكننا أن نعدل مصطلح “كمية حرة” إلى “العدد” من نافذة “الإعدادات العامة” من صفحة “المصطلحات” كما في الشكل التالي:




